Question: How do we use the other definitions of transformations?

Answer: You may ask: Didn't we learn all we had to learn about transformations? o.O
And the answer is, not yet. :(
But don't worry, we are almost there! :D
There are only three more things that we must discuss about transformations, they are:
                               Glide Reflection, Orientation, and Isometry. 

Lets start with glide reflection. What is glide reflection?
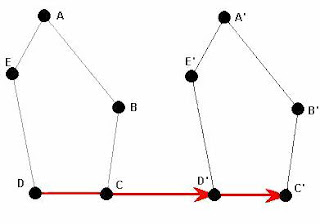
Glide reflection is the combination of a reflection in a line and a translation along that line.

Figure 1. This is an example of a glide reflection.

Figure 1 illustrates how the Figure was translated to the right and then reflected over the line.

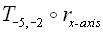Figure 2. This is how a glide reflection would be written out.

IMPORTANT: Whenever you solve a glide reflection, order doesn't matter, it is not like compositions of transformations where you have to start with the second transformation. In glide reflection, you can start with any transformation first.

Okay now lets move on into isometry. So what is isometry? 

Isometry, which is also referred to as isometric transformation, is a transformation of the plane that preserves length.  

What does that mean? Well that means that a figure can be moved around on a plane and as long as the length of the sides of the figure are the same, then it is an isometry. Lets look at an example:

Figure 3. The original triangle has gone through various transformations but the length of the sides have not changed so it is an isometry.

Now lets go over Orientation. What is orientation? 

Orientation refers to the arrangement of points, relative to another.

When orientation is preserved it is called a direct isometry. This means that the order of the letters on the diagram go in the same clockwise or counterclockwise on the figure and its image.

Figure 4. A translation is an example of a direct isometry because the order of the letter on the figure and image go in the same counterclockwise direction (orientation preserved).

 An opposite isometry changes the order (clockwise turns into counterclockwise).

Figure 5. Reflection is an example of opposite isometry because the order of the letters went from counterclockwise to clockwise (orientation not preserved).

NOW YOU TRY! :D

A triangle has vertices A(3,2), B(4,1) and C(4,3).  

What are the coordinates of point B under a glide reflection: 
 ?

1) (2,-4)

2) (4,0)

3) (4,-2)

4) (-4,2)

Question: How do we graph dilations?

Answer: So do you remember what a dilation is? If not then let me explain :)

A dilation is a type of transformation that causes an image to stretch or shrink in proportion to its original size. 

Okay now that we reviewed what a dilation is, lets go more in depth about dilations. :D

Whenever you do a dilation there will always be a scale factor.

So what's a scale factor? 

Well, a scale factor is the ratio by which the image stretches or shrinks. 

So how do we know if the figure will shrink or enlarge? o.O

Easy, if the scale factor is greater than one, then the image is enlarged.

          If written out, the scale factor would look like this --> D2

And if the scale factor is greater than zero but less than one, then the image will shrink. 

          If written out, the scale factor would look like this --> D1/4

Ok so now that we know how a dilation looks like, and what a scale factor is. So how do we solve a dilation problem? 

Well, all you have to do is multiply the dimensions of the original image by the scale factor to get the dimensions of the dilated image. 

For example: If we have a Triangle A(1,2) B(2,3) C(3,2) and a scale factor of D2 all we have to do to solve this problem is multiply the coordinate point of the triangle by the scale factor. This means:

2x(1,2)=(2,4)        so the image point A would be (2,4)

2x(2,3)=(4,6)        the image point B would be (4,6)

2x(3,2)=(6,4)        and the image point C would be (6,4)

NOW YOU TRY! :D

Given point A(6,5) and scale factor D3 what would be the image point?

Question: How do we solve composition of transformation problems?

Answer: Ok, first of all, lets go over what a composition of transformation is.
A composition of transformation is when two or more transformations are combined to form a new transformation.

Figure 1. This is how a composition of transformations is written out.

Now that we know what a composition of transformation is, lets go over how to solve it.
In order to solve a composition of transformation problem you must begin by solving the second transformation and then solving the first transformation.
It's a bit confusing so lets look at a picture:

Figure 2.

Ok so now that we have a picture to look at, we have a better idea on how to solve a composition of transformations problem.
As seen in Figure 2, begin with Translation(3,4) and then do reflection over the x-axis.

LETS SEE IF YOU GOT IT :)


Given Shape A(1,2) B(3,2) C(2,6), solve the following transformation:

 

Question: How do we graph transformations that are reflections?

Answer: Ok first off, lets review what a reflection is:

A reflection is a figure that is flipped over a line of symmetry.
Ok now that we know what a reflection is we must learn that there are two types of reflecions.
There is line symmetry(AKA reflectional symmetry) which is when a line can be drawn down a figure and divide it into identical images.

FIgure 1. Ex. this dog is an example of reflectional symmetry

Then there's line reflection, which is when a figure is flipped over a line to create two mirror images.

Figure 2. this is is an example of line reflection because the car itself is not split into two but there is a line from which the car is flipped over which creates a mirror image of the car.

Ok now that we are familiar with the types of reflections, let's learn how to graph them.
There are rules to follow when using reflection:
When you reflect over x-axis, the x coordinate point stays the same but the y coordinate point changes.
This means: (x,y) turns into --> (x,-y)
And when you reflect over the y-axis, the y coordinate stays the same but the x coordinate point changes.
This means: (x,y) turns into --> (-x,y)

NOW LET'S LOOK AT IT VISUALLY:

Point A was reflected over the x-axis which means that the x point will stay the same but the y point will change. In other words, (2,1) became (2,-1).

NOW YOU TRY! :D

If Point A(13,-5) is reflected over the x-axis, where would point A' be?

                              A)  (13,-5)                                             C) (13,5)
                              B)  (-13,5)                                             D) (-13.-5)

How do we identify transformations?

Question: So what is a transformation? o.O

Answer: Simple, a transformation is when you move a goemetric figure :D

Now there are four types of transformations: Translation, Reflection, Rotation, and Dilation.

A translation is when every point is moved the same distance in the same direction.

Figure 1 Ex. Triangle ABC was translated (or moved) six units to the right and four units down. 

Translations are written with a capital T. Figure 1 for example, would be written as T(6,-4)

A reflection is when a figure is flipped over a line of symmetry.

Figure 2 Ex. The letter E was flipped over a line of reflection. The line of reflection acts like a mirror.

Reflections are written as lower case r's. Ex. r(x-axis)

A rotation is when a figure is turned around a single point.

Figure 3 Ex. Shape A was rotated along the point O.

Rotations are written out using a capital R followed by the degree of the rotation. Ex. R90*

A dilation is when an  image is reduced or enlarged in size.

Figure 4 Ex. This little tiger was enlarged to double its original size.

Dilations are written out with a capital D followed by the amount of enlargement or reduction. Ex. D2


NOW YOU TRY! :D

Figure 5

What type of transformation is Figure 5?
A) Reflection
B)Rotation
C)Dilation
D)Translation