Answer: So first of all what are prisms and cylinders?
Well prisms are solids with bases that are two congruent polygons. And a cylinder is a solid with two congruent circular bases connected by a tube.
So how do you find the lateral area?
To find the lateral area of a prism you multiply the perimeter by the height. Formula--> L.A.=Ph
This formula represents P as the perimeter of one of the bases and h as the height.
To find the lateral area of a prism you multiply the radius of one of the bases times two then multiply it by the height and finally multiply it by π. Formula--> L.A.=2πrh
And how do you find the volume?
To find the volume of a prism you multiply the base times the height. Formula--> V=Bh
This formula represents B as the base area and h as the height.
To find the volume of a cylinder you multiply the radius by itself and then times it by the height and finally multiply it by π.
NOW YOU TRY! :D
What is the area of the following prism?
Sunday, April 1, 2012
Question: How do we identify solids?
Answer: A solid, which is also known as a 3D object because it has three dimensions: width, depth, and height.
Solids have two properties that make them solids: they have surface area and volume.
Volume is the space inside an object, and surface area is the outer measurement of the object.
Okay, so now let me tell you that there are two different types of solids: Polyhedra and Non-Polyhedra.
The rule for Polyhedra solids is that all the sides must be flat surfaces.
Examples of these types of solids are shown below:
The rule for Non-Polyhedra is the opposite, if one or more of the sides is curved then it is a non-polyhedra.
Examples of these types of solids are shown below:
NOW YOU TRY! :D
What type of solid is the shape below?
Solids have two properties that make them solids: they have surface area and volume.
Volume is the space inside an object, and surface area is the outer measurement of the object.
Okay, so now let me tell you that there are two different types of solids: Polyhedra and Non-Polyhedra.
The rule for Polyhedra solids is that all the sides must be flat surfaces.
Examples of these types of solids are shown below:
The rule for Non-Polyhedra is the opposite, if one or more of the sides is curved then it is a non-polyhedra.
Examples of these types of solids are shown below:
NOW YOU TRY! :D
What type of solid is the shape below?
Sunday, March 25, 2012
Question: How do we find the area of a circle?
Answer: That's very easy, the area of a circle is given by the formula A= πr2(squared) where A is the area and r is the radius.
P.s. sometimes the radius isn't given to you, instead you are given the diameter. But dont worry because the diameter is just the radius times 2. So all you need to do to find the radius is divide the diameter by two! :)
NOW YOU TRY! :D
Find the area of the circle:
NOW YOU TRY! :D
Find the area of the circle:
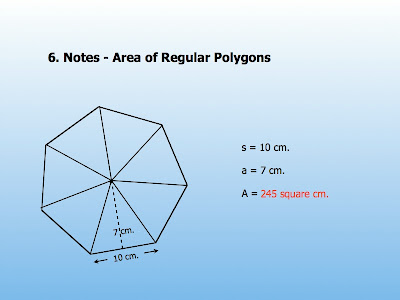
Question: How do we find the area of regular polygons?
Answer: Well you can divide a regular polygon into congruent isosceles triangles by drawing segments to each vertex, as shown in the following figure:
Regular Polygon Area Conjecture
The area of a regular polygon is given by the formulas: A=nas and A=Pa
2 2
Where A is the area, P is the Perimeter, a is the apothem, s is the length of sides, and n is the number of sides.
The apothem is the perpendicular bisector from the center of the polygon to the side.
As seen in the image above, to find the area all you have to do is follow either one of the formulas, right now i am going to use the formula: A=nas
2
So i will have to multiply 7(n) times 7(a) times 10(s) and divide it by 2. Thus, the area of the heptagon will be 245 square cm.
NOW YOU TRY! :D
Find the area of the following polygon:
Regular Polygon Area Conjecture
The area of a regular polygon is given by the formulas: A=nas and A=Pa
2 2
Where A is the area, P is the Perimeter, a is the apothem, s is the length of sides, and n is the number of sides.
The apothem is the perpendicular bisector from the center of the polygon to the side.
As seen in the image above, to find the area all you have to do is follow either one of the formulas, right now i am going to use the formula: A=nas
2
So i will have to multiply 7(n) times 7(a) times 10(s) and divide it by 2. Thus, the area of the heptagon will be 245 square cm.
NOW YOU TRY! :D
Find the area of the following polygon:
Question: How do we find the area of parallelograms, kites, and trapezoids.
Answer: Woah that's a lot of shapes! :O
So lets start of with parallelograms :) and lets review what area is, area is the space inside a shape.
Okay so now, to find the area of a parallelogram you must multiply the base times the height. Its very similar to finding the area of a rectangle :) AREA=B*H
Okay lets move on into trapezoids:
To find the area of a trapezoid, you must add the two bases and divide them by two, then you multiply it by the height. It sounds a bit confusing so lets look at it visually :)
Finally. lets learn how to find the area of a kite:
To find the area of a kite you must multiply the two diagonals and divide them by two.
NOW YOU TRY! :D
Find the area of the following figure:
So lets start of with parallelograms :) and lets review what area is, area is the space inside a shape.
Okay so now, to find the area of a parallelogram you must multiply the base times the height. Its very similar to finding the area of a rectangle :) AREA=B*H
Okay lets move on into trapezoids:
To find the area of a trapezoid, you must add the two bases and divide them by two, then you multiply it by the height. It sounds a bit confusing so lets look at it visually :)
Finally. lets learn how to find the area of a kite:
To find the area of a kite you must multiply the two diagonals and divide them by two.
NOW YOU TRY! :D
Find the area of the following figure:
Question: How do we calculate the are of rectangles and triangles?
Answer: First of all what is area?
The area of a figure is the measure region enclosed by the figure.
Okay now that we know what area is, lets find out how to find the area of a rectangle! :D
The area of a rectangle can be found by multiplying the length(L) times the width(W). AREA=L*W
The area is measured in "units squared." If your rectangle is 5 inches long and 3 inches wide, to find the area you must multiply these two. so it would be: 5inches * 3 inches = 15inches(squared). Illustrated in Figure 1.
The area of a figure is the measure region enclosed by the figure.
Okay now that we know what area is, lets find out how to find the area of a rectangle! :D
The area of a rectangle can be found by multiplying the length(L) times the width(W). AREA=L*W
 |
| Figure 1 |
Now lets find out how to find the area of a triangle. To find the area of a triangle you do one half the base times the height. AREA=(1/2)B*H
NOW YOU TRY! :D
Find the area of the rectangle above.
Thursday, March 15, 2012
Question: How do we solve logic problems using conditionals?
Answer: I have already stated what a math statement is, but if you don't remember then i shall refresh your memory :)
A mathematical statement is a statement that can be judged to be true or false.
Ok now that we have gone over math statements, lets go over conditional.
A conditional falls under the category of logic in geometry. a conditional is a compound sentence created by putting together two sentences using the words "IF" and "THEN." A conditional is also made up of a hypothesis and a conlusion.
Example:
If I am laughing
then I am having fun
-The hypothesis of this conditional is "i am laughing" and the conclusion is "i am having fun."
NOW YOU TRY! :D
Form a conditional out of the following hypothesis and conclusion:
Hypothesis- it is raining
Conclusion- i will take my umbrella
Question: How do we find compound loci?
Answer: Ok so we already know what loci is, now what is a compound loci?
Well a compound locus problem involves two or more locus conditions in one problem. The way to differentiate a compound locus problem from a regular locus problem is by the words "AND" and "AND ALSO."
Example Problem:
A treasure is buried in your backyard. The picture below shows your backyard which contains a stump, a teepee, and a tree. The teepee is 8 feet from the stump and 18 feet from the tree. The treasure is equidistant from the teepee and the tree AND ALSO 6 feet from the stump. Locate all possible points of the buried treasure. (Figure 1)
Step 1:
Ok first read the problem and determine ONE of the locus conditions.
Step 2:
Solve the first locus solution and plot it.
Step 3:
Re-read the problem and identify the second locus condition.
Step 4:
Solve the second locus solution and plot it.
Ok so now lets see this would look like: (Figure 2)
Explanation of Solutions:
The red line represents the locus which is equidistant from the teepee and the tree (the perpendicular bisector of the segment AKA the first locus condition). The blue circle represents the locus which is 6 feet from the stump (the second locus condition). These two loci intersect in two locations. The treasure could be buried at either "X" location.
NOW YOU TRY! :D
Two points A and B are 6 units apart. How many points are there that are equidistant from both A and B and also 5 units from A?
1. 1
2. 2
3. 3
4. 4
Well a compound locus problem involves two or more locus conditions in one problem. The way to differentiate a compound locus problem from a regular locus problem is by the words "AND" and "AND ALSO."
Example Problem:
A treasure is buried in your backyard. The picture below shows your backyard which contains a stump, a teepee, and a tree. The teepee is 8 feet from the stump and 18 feet from the tree. The treasure is equidistant from the teepee and the tree AND ALSO 6 feet from the stump. Locate all possible points of the buried treasure. (Figure 1)
 |
| Figure 1 |
Step 1:
Ok first read the problem and determine ONE of the locus conditions.
Step 2:
Solve the first locus solution and plot it.
Step 3:
Re-read the problem and identify the second locus condition.
Step 4:
Solve the second locus solution and plot it.
Ok so now lets see this would look like: (Figure 2)
 |
| Figure 2 |
The red line represents the locus which is equidistant from the teepee and the tree (the perpendicular bisector of the segment AKA the first locus condition). The blue circle represents the locus which is 6 feet from the stump (the second locus condition). These two loci intersect in two locations. The treasure could be buried at either "X" location.
NOW YOU TRY! :D
Two points A and B are 6 units apart. How many points are there that are equidistant from both A and B and also 5 units from A?
1. 1
2. 2
3. 3
4. 4
Question: How do we find the locus of points?
Answer: So what is a locus? Well a locus is the set of all points that satisfy a given condition.
The plural of locus is loci
Ok now, let me explain how to identify the different types of locus problems.
There are 5 types of locus problems.
LOCUS PROBLEM #1: Finding the locus of one point
 |
| Figure 1 |
Whenever you are trying to find the locus of one point, the loci will be equidistantly away from the point. In figure 1, for example, the locus of points away from point P will be an equal distance away from the point, thus it will produce a circle with the original point (P) in the center.
LOCUS PROBLEM #2: Finding the locus of two points
 |
| Figure 2 |
Whenever you are trying to find the locus of two points, the loci will be a line through the middle of the two points. As illustrated in figure 2, for example, the locus of points away from points P and Q will be the perpendicular bisector of the line segment connecting the two points.
LOCUS PROBLEMS #3: Finding the locus of a line
 |
| Figure 3 |
Whenever you are trying to find the locus of a line, the loci will be two parallel lines on opposite sides of te original line. As illustrated in figure 3, for example, the locus of points of line L will be two lines, opposite sides, equidistant and parallel to the original line.
LOCUS PROBLEM #4: Finding the locus of two lines
 |
| Figure 4 |
Whenever you are trying to find the locus of two lines, the loci will be a line through the middle of the two lines. As illustrated in figure 4, for example, the locus of points of lines L1 and L2 will be another line halfway between both lines, and parallel to each other.
LOCUS PROBLEM #5: Finding the locus of two intersecting lines
 |
| Figure 5 |
Whenever you are trying to find the locus of two intersecting lines, the loci will be two intersecting lines halfway between the two original lines. As illustrated in figure 5, for example, the locus of points of lines L1 and L2 will be two additional lines that bisect the angles formed by the original lines.
NOW YOU TRY! :D
What shape would the locus of points 3 inches away from point A form?
1.A circle
2.A square
3.A triangle
4.A rhombus
Saturday, March 3, 2012
Question: What is a mathematical statement?
Answer: A mathematical statement is a statement that can be judged to be true or false.
Ex. John Kennedy was a U.S. President.
Now lets go over negations.
Negations (not) always adds the opposite truth value to a mathematical statement.
Ex. John Kennedy was not a U.S. President.
When dealing with mathematical statements, we will usually look at more than one statement.
And since we will be dealing with multiple we must know what conjunctions are.
Conjunctions connect two statements with words such as and, but, or.
Ex. The President of the U.S. is Barack Obama and the vice president is Joe Biden.
And - both statements must be true for the statement to be true
Ex. I'm going to have pizza or tacos for dinner.
Or - Either statement (or both) can be true for the statement to be true.
Now let's talk about conditionals. The conditional is the most frequently used statement in the construction of an argument or in the study of mathematics (geometric proofs). There are four types of conditionals:
-Conditional
-Converse
-Inverse
-Contrapositive
NOW YOU TRY! :D
Is the following a mathematical statement?
An owl is a fish. Yes or no?
Ex. John Kennedy was a U.S. President.
Now lets go over negations.
Negations (not) always adds the opposite truth value to a mathematical statement.
Ex. John Kennedy was not a U.S. President.
When dealing with mathematical statements, we will usually look at more than one statement.
And since we will be dealing with multiple we must know what conjunctions are.
Conjunctions connect two statements with words such as and, but, or.
Ex. The President of the U.S. is Barack Obama and the vice president is Joe Biden.
And - both statements must be true for the statement to be true
Ex. I'm going to have pizza or tacos for dinner.
Or - Either statement (or both) can be true for the statement to be true.
Now let's talk about conditionals. The conditional is the most frequently used statement in the construction of an argument or in the study of mathematics (geometric proofs). There are four types of conditionals:
-Conditional
-Converse
-Inverse
-Contrapositive
NOW YOU TRY! :D
Is the following a mathematical statement?
An owl is a fish. Yes or no?
Question: What is logic?
Answer: LOGIC IS THINKING!!!
Logic is simply a tool that we use to determine between true or false.
For example, we all use logic every single day.
Logic is kind of like common sense.
When you come to a busy street and you decide whether to cross or not, then you are using logic.
There is also inductive reasoning.
Inductive reasoning is when you use prior knowledge to predict the future (it might not always be true).
NOW YOU TRY! :D
How have you used logic today?
Logic is simply a tool that we use to determine between true or false.
For example, we all use logic every single day.
Logic is kind of like common sense.
When you come to a busy street and you decide whether to cross or not, then you are using logic.
There is also inductive reasoning.
Inductive reasoning is when you use prior knowledge to predict the future (it might not always be true).
NOW YOU TRY! :D
How have you used logic today?
Sunday, February 26, 2012
Question: How do we use the other definitions of transformations?
Answer: You may ask: Didn't we learn all we had to learn about transformations? o.O
And the answer is, not yet. :(
But don't worry, we are almost there! :D
There are only three more things that we must discuss about transformations, they are:
Glide Reflection, Orientation, and Isometry.
Lets start with glide reflection. What is glide reflection?
Glide reflection is the combination of a reflection in a line and a translation along that line.
Figure 1 illustrates how the Figure was translated to the right and then reflected over the line.
And the answer is, not yet. :(
But don't worry, we are almost there! :D
There are only three more things that we must discuss about transformations, they are:
Glide Reflection, Orientation, and Isometry.
Lets start with glide reflection. What is glide reflection?
Glide reflection is the combination of a reflection in a line and a translation along that line.
 |
| Figure 1. This is an example of a glide reflection. |
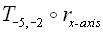 |
| Figure 2. This is how a glide reflection would be written out. |
IMPORTANT: Whenever you solve a glide reflection, order doesn't matter, it is not like compositions of transformations where you have to start with the second transformation. In glide reflection, you can start with any transformation first.
Okay now lets move on into isometry. So what is isometry?
Isometry, which is also referred to as isometric transformation, is a transformation of the plane that preserves length.
What does that mean? Well that means that a figure can be moved around on a plane and as long as the length of the sides of the figure are the same, then it is an isometry. Lets look at an example:
 |
| Figure 3. The original triangle has gone through various transformations but the length of the sides have not changed so it is an isometry. |
Now lets go over Orientation. What is orientation?
Orientation refers to the arrangement of points, relative to another.
When orientation is preserved it is called a direct isometry. This means that the order of the letters on the diagram go in the same clockwise or counterclockwise on the figure and its image.
 |
| Figure 4. A translation is an example of a direct isometry because the order of the letter on the figure and image go in the same counterclockwise direction (orientation preserved). |
An opposite isometry changes the order (clockwise turns into counterclockwise).
 |
| Figure 5. Reflection is an example of opposite isometry because the order of the letters went from counterclockwise to clockwise (orientation not preserved). |
NOW YOU TRY! :D
A triangle has vertices A(3,2), B(4,1) and C(4,3).
What are the coordinates of point B under a glide reflection:
 ?
?
 ?
?
1) (2,-4)
2) (4,0)
3) (4,-2)
4) (-4,2)
Question: How do we graph dilations?
Answer: So do you remember what a dilation is? If not then let me explain :)
For example: If we have a Triangle A(1,2) B(2,3) C(3,2) and a scale factor of D2 all we have to do to solve this problem is multiply the coordinate point of the triangle by the scale factor. This means:
A dilation is a type of transformation that causes an image to stretch or shrink in proportion to its original size.
Okay now that we reviewed what a dilation is, lets go more in depth about dilations. :D
Whenever you do a dilation there will always be a scale factor.
So what's a scale factor?
Well, a scale factor is the ratio by which the image stretches or shrinks.
So how do we know if the figure will shrink or enlarge? o.O
Easy, if the scale factor is greater than one, then the image is enlarged.
If written out, the scale factor would look like this --> D2
And if the scale factor is greater than zero but less than one, then the image will shrink.
If written out, the scale factor would look like this --> D1/4
Ok so now that we know how a dilation looks like, and what a scale factor is. So how do we solve a dilation problem?
Well, all you have to do is multiply the dimensions of the original image by the scale factor to get the dimensions of the dilated image.
For example: If we have a Triangle A(1,2) B(2,3) C(3,2) and a scale factor of D2 all we have to do to solve this problem is multiply the coordinate point of the triangle by the scale factor. This means:
2x(1,2)=(2,4) so the image point A would be (2,4)
2x(2,3)=(4,6) the image point B would be (4,6)
2x(3,2)=(6,4) and the image point C would be (6,4)
NOW YOU TRY! :D
Given point A(6,5) and scale factor D3 what would be the image point?
Question: How do we solve composition of transformation problems?
Answer: Ok, first of all, lets go over what a composition of transformation is.
A composition of transformation is when two or more transformations are combined to form a new transformation.
Now that we know what a composition of transformation is, lets go over how to solve it.
In order to solve a composition of transformation problem you must begin by solving the second transformation and then solving the first transformation.
It's a bit confusing so lets look at a picture:
Ok so now that we have a picture to look at, we have a better idea on how to solve a composition of transformations problem.
As seen in Figure 2, begin with Translation(3,4) and then do reflection over the x-axis.
LETS SEE IF YOU GOT IT :)
Given Shape A(1,2) B(3,2) C(2,6), solve the following transformation:
A composition of transformation is when two or more transformations are combined to form a new transformation.
 |
| Figure 1. This is how a composition of transformations is written out. |
Now that we know what a composition of transformation is, lets go over how to solve it.
In order to solve a composition of transformation problem you must begin by solving the second transformation and then solving the first transformation.
It's a bit confusing so lets look at a picture:
 |
| Figure 2. |
As seen in Figure 2, begin with Translation(3,4) and then do reflection over the x-axis.
LETS SEE IF YOU GOT IT :)
Given Shape A(1,2) B(3,2) C(2,6), solve the following transformation:
Saturday, February 25, 2012
Question: How do we graph transformations that are reflections?
Answer: Ok first off, lets review what a reflection is:
A reflection is a figure that is flipped over a line of symmetry.
Ok now that we know what a reflection is we must learn that there are two types of reflecions.
There is line symmetry(AKA reflectional symmetry) which is when a line can be drawn down a figure and divide it into identical images.
Then there's line reflection, which is when a figure is flipped over a line to create two mirror images.
Ok now that we are familiar with the types of reflections, let's learn how to graph them.
There are rules to follow when using reflection:
When you reflect over x-axis, the x coordinate point stays the same but the y coordinate point changes.
This means: (x,y) turns into --> (x,-y)
And when you reflect over the y-axis, the y coordinate stays the same but the x coordinate point changes.
This means: (x,y) turns into --> (-x,y)
NOW LET'S LOOK AT IT VISUALLY:
NOW YOU TRY! :D
A) (13,-5) C) (13,5)
B) (-13,5) D) (-13.-5)
A reflection is a figure that is flipped over a line of symmetry.
Ok now that we know what a reflection is we must learn that there are two types of reflecions.
There is line symmetry(AKA reflectional symmetry) which is when a line can be drawn down a figure and divide it into identical images.
 |
| FIgure 1. Ex. this dog is an example of reflectional symmetry |
Then there's line reflection, which is when a figure is flipped over a line to create two mirror images.
 |
| Figure 2. this is is an example of line reflection because the car itself is not split into two but there is a line from which the car is flipped over which creates a mirror image of the car. |
There are rules to follow when using reflection:
When you reflect over x-axis, the x coordinate point stays the same but the y coordinate point changes.
This means: (x,y) turns into --> (x,-y)
And when you reflect over the y-axis, the y coordinate stays the same but the x coordinate point changes.
This means: (x,y) turns into --> (-x,y)
NOW LET'S LOOK AT IT VISUALLY:
 |
| Point A was reflected over the x-axis which means that the x point will stay the same but the y point will change. In other words, (2,1) became (2,-1). |
NOW YOU TRY! :D
 |
| If Point A(13,-5) is reflected over the x-axis, where would point A' be? |
B) (-13,5) D) (-13.-5)
Monday, February 6, 2012
How do we identify transformations?
Question: So what is a transformation? o.O
Answer: Simple, a transformation is when you move a goemetric figure :D
Now there are four types of transformations: Translation, Reflection, Rotation, and Dilation.
A translation is when every point is moved the same distance in the same direction.
Translations are written with a capital T. Figure 1 for example, would be written as T(6,-4)
A reflection is when a figure is flipped over a line of symmetry.
Reflections are written as lower case r's. Ex. r(x-axis)
A rotation is when a figure is turned around a single point.
Rotations are written out using a capital R followed by the degree of the rotation. Ex. R90*
A dilation is when an image is reduced or enlarged in size.
Dilations are written out with a capital D followed by the amount of enlargement or reduction. Ex. D2
NOW YOU TRY! :D
What type of transformation is Figure 5?
A) Reflection
B)Rotation
C)Dilation
D)Translation
Answer: Simple, a transformation is when you move a goemetric figure :D
Now there are four types of transformations: Translation, Reflection, Rotation, and Dilation.
A translation is when every point is moved the same distance in the same direction.
 |
| Figure 1 Ex. Triangle ABC was translated (or moved) six units to the right and four units down. |
A reflection is when a figure is flipped over a line of symmetry.
 |
| Figure 2 Ex. The letter E was flipped over a line of reflection. The line of reflection acts like a mirror. |
A rotation is when a figure is turned around a single point.
 |
| Figure 3 Ex. Shape A was rotated along the point O. |
A dilation is when an image is reduced or enlarged in size.
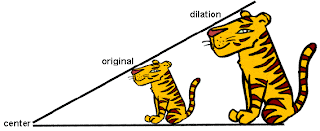 |
| Figure 4 Ex. This little tiger was enlarged to double its original size. |
NOW YOU TRY! :D
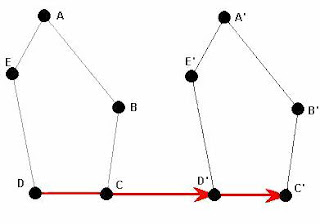 |
| Figure 5 |
A) Reflection
B)Rotation
C)Dilation
D)Translation
Subscribe to:
Comments (Atom)